A team at NUS Institute for Functional Intelligent Materials, together with international collaborators, developed a machine learning approach for fast and data-efficient prediction of properties of defects in 2D materials .
2D materials offer exciting opportunities as building blocks for new electronic devices, such as bendable screens, efficient solar panels, and high-resolution cameras. Imperfections and defects radically change the electronic properties of 2D materials. They can turn insulators into semiconductors, semiconductors to metals, make materials magnetic or catalytic.
The developed method and its software implementation allow for fast and accurate property prediction, providing a staging ground for automated material design for those purposes. It has been recently published as Sparse representation for machine learning the properties of defects in 2D materials.
Designing new materials: from alchemy to AI
Designing a new material is somewhat similar to creating a new dish; it consists of trial-and-error procedure repeated until success. Throughout most of history, it was conducted with traditional bench experiments. Like alchemists of the old, people were guided by intuition and tried different components and recipes to create new materials for buildings and weapons. Mixing arsenic with mercury in an attempt to create gold is, of course, fun. However it is not only dangerous, but also very slow and labor intensive.
The second half of the 20th century saw the rise of computational methods. The Nobel Prize in Chemistry 1998 was awarded for the development of the density functional theory – a method widely used today. It became possible to do computational experiments instead of real ones. Instead of actually synthesizing and analyzing material candidates, scientists can run programs that would predict the properties of these candidates. The main limiting factor is the computational cost. Algorithms based on faithfully applying the laws of quantum mechanics take hours and days to run. It is still a breakthrough from weeks and months of experiment work, of course. However, the number of possible candidate materials is practically infinite. For example, you can take the figure below, and change every atom into some other element from the periodic table – just imagine how many options there are. So hours of computation are still not good enough.
Machine learning (ML) is an emergent solution. It allows computers to have an intuition, to guess the properties of material by just looking at it. After investing in the computations to create the training dataset, and training a model, predictions can be obtained at least 1000 times faster, thus allowing 1000 times faster exploration.
2D materials with defects
Ideal crystalline materials consist of an infinite repeating pattern. Real crystalline materials have defects. In our work we study point defects: vacancies, when an atom is removed, and substitutions, when an atom is replaced with a different one. Defects dramatically affect the properties of materials. For example, steel is iron with added carbon. Just 1-2% of its mass is carbon, but you can’t build a skyscraper without it. For 2D materials, the effect is much more profound. A small empty bubble deep inside a metal cube won’t change it much, but a hole in a metal sheet allows the light to shine through. Same holds true on the microscopic level.
For example, adding holes to boron nitride sheet turns it from insulating to conducting! Check for ion bombardment and electron irradiation before making a power plug out of it. And just 2% of defects reduce the mechanical strength by 50%.

Sparse representation
As the team discovered, current ML methods perform poorly in the task of predicting interactions of multiple defects. The algorithms are just not attentive enough to notice the small differences. Since the AI had no childhood, it had no opportunity to play “Spot the Difference” enough. The researchers proposed to help the algorithm by highlighting the important parts of structures. They called it a sparse representation of the structure with defects. A rough analogy would be this. A football coach (the algorithm) needs to analyze and understand the strategy of an opposing team (full structure of a 2D material) to come up with a winning game plan. Watching every single game the opponent has ever played would be incredibly laborious and time-consuming. Instead, the coach could watch selected highlights or specific plays (sparse representation) that illustrate the team’s strengths and weaknesses (defects). This approach retains almost all necessary information about the opposing team while significantly reducing the time and complexity of the problem. The real process of obtaining the representation is depicted below:
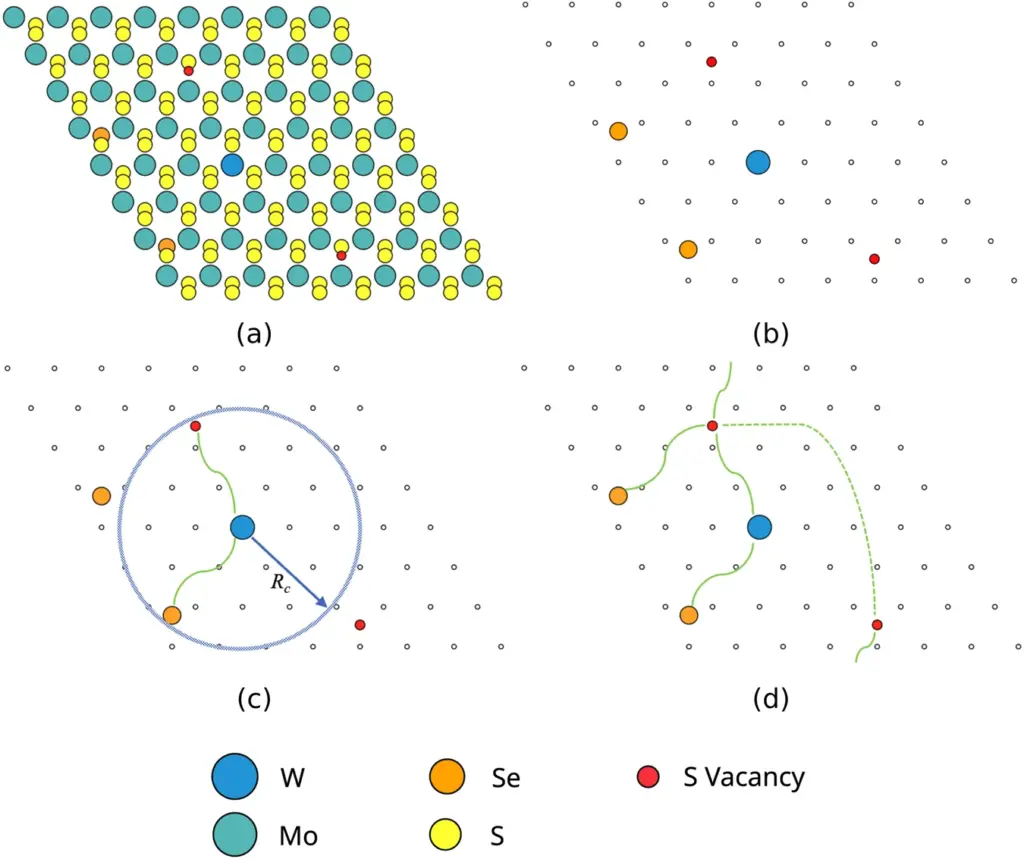
(a) Start with a full structure of a 2D material with defects
(b) Get the sparse structure by removing the sites that don’t contain defects
(c) A graph built by connecting the defect sites that are closer than the cutoff radius
(d) Resulting sparse graph. Note the edges going through the periodic boundary
The sparse representation retains almost all information about the structure, while reducing the dimensionality of the problem almost 100-fold. This results in much more accurate predictions, with mean absolute error reduction by a factor of at least 3.7 compared to current machine learning methods.
